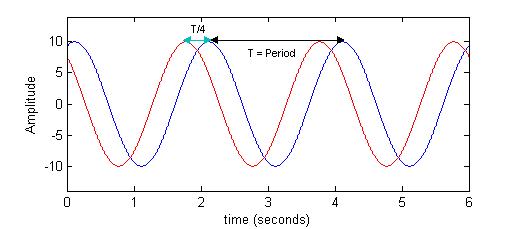
Here's a link to a youtube video on using the animation below which also discusses angular velocity and relates the animation to the mathematics.All sinusoidal wavforms have the same basic shape but can differ in amplitude, frequency and phase.
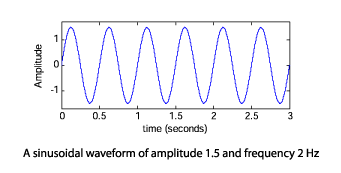
In the example to the right the amplitude is 1.5 and the frequency is 2 Hz (2 cycles per second); I'll deal with phase later. The period in seonds is equal to 1/frequency, so its 0.5 seconds in this case.
You should try changing the parameters of the sinusoid in the animation below to make sure you fully understand the effect of changing the amplitude and frequency. You should also notice that if you change the phase offset then the times when the sinusoid reaches a maximum will also change. Check out the section on the mathematics to get a full explanation.
check to show calculations
y(t) = Asin(2πft + φ) , where A represents amplitude, f represents frequency and φ represents phase offset, and t represents time.If you subsituted A with 1.5, f with 0.5, and φ with 0, you'd be left with the following expression:
y(t) = 1.5sin(πt)If you then evaluated this expression for t = 0, 0.1, 0.2, ... ..., 2.9, 3 and then plotted y(t) against t you'd get the plot show in the top right of this page. You should try changing the sinusoidal parameters in the animation to these values and check the 'show calculations' box to see this expression being evaluated.
As you can see in the animation, sinusoids are associated with a rotating vector which rotates at a particular angluar speed ω. You can see that the vector undergoes a rotation of 2π radians for every one cycle of the sinusoidal waveform. It therefore follows if the sinudoidal waveform has a frequency of 1 Hz the associated rotating vector has an anglular speed of 2π radians per second. In more general terms the angular speed ω has the following relationship with sinusoidal frequency f:
ω = 2πfIt is very common for sinusoidal frequency to be expressed both in terms of Hertz and radians per second (rads/s) and it is important to be comfortable with both. You will also see sinusoids described mathematically using angular velocity as follows:
y(t) = Asin(ωt + φ)Another common way to see a sinusoidal waveform expressed is by using a cosine function rather than a sine function i.e.
y(t) = Acos(2πft + φ) = Acos(ωt + φ)Since cos(x) = sin(x + π/2) then
y(t) = Acos(ωt + φ) = Asin(ωt + φ + π/2)
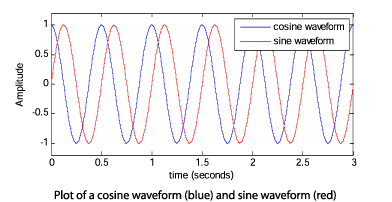A cosine waveform is described mathematically by:
y(t) = Acos(ωt)and a sine waveform is given by:
y(t) = Asin(ωt)Since Acos(ωt) = Asin(ωt + π/2) there is said to be phase difference of π/2 radians between the two waveforms. The phase difference can also be thought of as being one quarter of a cycle between the sinusoids since there are 2π radians in one complete cycle of a sinusoid and π/2 corresponds to one quarter of a complete cycle of a sinusoid.
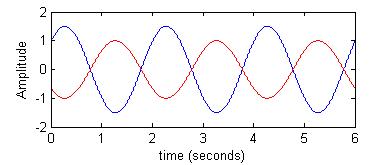If you have two sinusoids of the same frequency but of different phase offset then there will be a phase difference between them. In the example to the right there is a phase difference of π between the two waveforms. It is also frequently said that there is a phase difference of a half cycle between the two waveforms.You could also say that there is a phase difference of -π between the two waveforms, as this is equivalent to a phase difference of π. Phase differences of 3π, -3π, 5π, -5π, would also be valid in this case but ususally phase difference (and phase offset) is expressed as some number the lies either between 0 and 2π or between -π and π
In the second example shown below the phase difference between the waveforms is one quarter of a cycle or pi/2 radians.
One interaction of particular interest is how sinusoids of the same frequency sum together (add and subtract). It's worth noting that when sinusoids of the same frequency are summed together that the frequency of the resulting sinusoid is the same frequency as the original sinusoids and that only the amplitude and phase will change. It turns out that we can use complex numbers to quickly and conveniently determine the amplitude of the resulting sinusoid. The process to doing this is described in the following paragraphs.
The first step is to represent each individual sinusoid using complex numbers. The way we do this is to set the magnitude of the complex number to be the amplitude of each sinusoid and then to set the angle of the complex number to be the phase offset of each sinusoid. So, in the example shown in the figure above, where the the sinusoids to be added are cos(10πt)+0.8) and 1.8cos(10πt-1.2), these sinusoids are represented, using angle notation, as the complex numbers 1∠0.8 (or 0.6967 + 0.7174i in rectangular form) and 1.8∠-1.2 ( or 0.6522 - 1.6777i).
The next step just involves adding these complex numbers together (This will work no matter how many sinusoids you are adding - or subtracting), which works out to be 1.3490 - 0.9603i in rectangular form (or 1.6559∠-0.6187 using angle notation). The magntiude of the resulting complex number is equal to the amplitude of the resulting sinusoid and the angle of the complex number is the phase of the resulting sinusoid. So it turns out that cos(10πt)+0.8)+1.8cos(10πt-1.2) = 1.6559cos(10πt-0.6187).